By Andrey Solovev, Chief Technology Officer, Integra Sources
One of the purposes of battery management systems is to monitor the state-of-charge and state-of-health of rechargeable batteries. This article will tell you about these two metrics and the methods used to measure them.
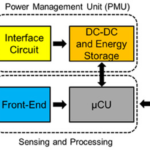
Rechargeable batteries are used in many solutions, but industries use battery management systems (BMSs) to increase their longevity and ensure safety. One of the ways to make sure a battery works longer is to oversee its state-of-charge (SOC) and state-of-health (SOH).
The state-of-charge shows how much energy is left in a battery (or the level of remaining capacity), telling a user when it needs to be recharged.
The state-of-health represents the level of deterioration of a battery that inevitably occurs as it ages, telling users when it needs to be replaced.
Thus, the SOC and SOH are two key metrics that reflect how batteries perform and predict their behavior. But there is no way to directly measure a battery’s SOC or SOH. Instead, engineers have to rely on indirect measuring methods.
Measuring a battery’s state-of-charge
The techniques applied for measuring the SOC bank on both direct and indirect calculations as well as prediction. Here are the most commonly used methods.
Open-circuit voltage (OCV) technique
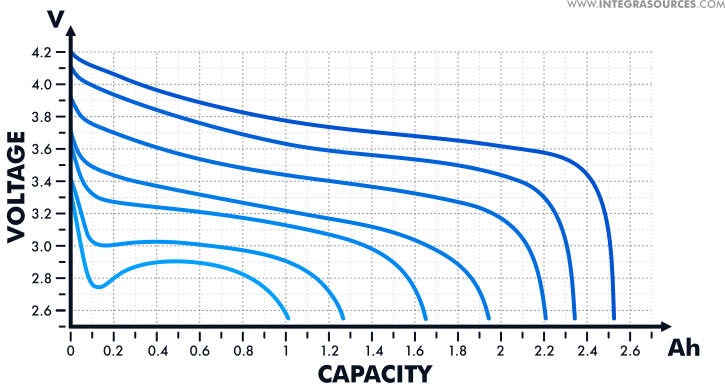
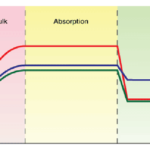
This method uses the variation in a battery’s state-of-charge to the open-circuit voltage. The stronger the difference between these two parameters, the higher level of accuracy one can achieve. Manufacturers usually provide this information in discharge curve tables.
Despite high accuracy, this method isn’t widely used in practice as one has to shut off the power completely and let the battery rest for up to several hours before measuring its SOC. So, unless the power consumption of your battery-powered system is negligibly low, using this technique to measure a battery’s SOC while in operation is impossible. Besides, it doesn’t suit Li-ion batteries since their discharge curve is relatively flat.
However, the OCV method works well for measuring the SOC of batteries that were stored for a long time or if the system was shut off for a while.
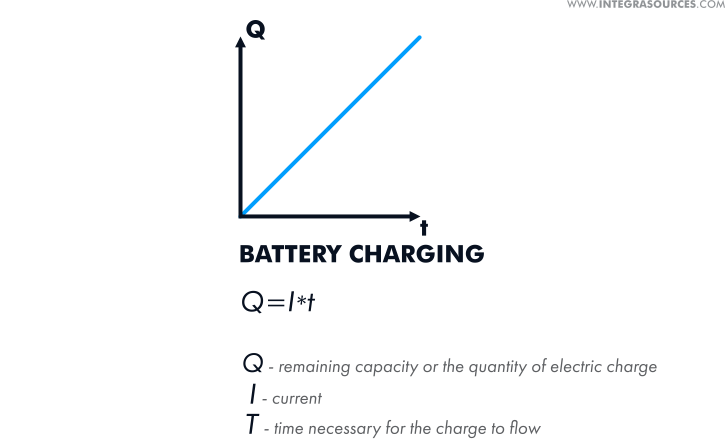
Coulomb counting (current integration)
This method aims to calculate the quantity of electric charge (measured in coulombs) added to a battery’s capacity when it’s being charged or extracted from a battery’s capacity when it’s being discharged.
This method has several drawbacks. First, the battery must be fully charged or discharged to show its initial state-of-charge to reach acceptable accuracy. Second, the coulomb counting technique requires correct, current measurement. It can be achieved either by using expensive current sensors or by averaging the collected data with Kalman filtering or neural networks.
Kalman filtering
The Kalman filtering algorithm uses current, voltage, internal resistance, temperature, and other data to simulate the battery’s behavior and operating conditions in an electrical model. Provided with a constant data flow, the algorithm corrects its predictions every second, resulting in precise estimations.
Modern BMSs usually use not one but several methods to estimate the SOC.
Measuring a battery’s state-of-health
The state-of-health reflects a battery’s deterioration level and is an even more abstract parameter than SOC. Nevertheless, it can be estimated by measuring related physical parameters.
Counting charge/discharge cycles
The easiest way to determine a battery’s degradation level is to simply count how many charge and discharge cycles it’s been through. In this case, engineers take the cycle life claimed by the manufacturer as a reference point.
But only Li-ion batteries show a direct relationship between their state-of-health and cycle life. Besides, the method doesn’t take into account certain factors, such as voltage and current, as well as the battery’s operating conditions that also influence its SOH.
Internal resistance measurement
A battery’s SOH is directly related to its internal resistance. The latter rises as a battery wears off.
One way to calculate it is to measure the difference between open-circuit voltage and voltage with the connected current load using Ohm’s law. But again, one can only measure a battery’s OCV when it’s at rest, so this technique has limited practical use.
An alternative solution is to measure the battery’s energy during operation and use Joule’s law or Electrochemical Impedance Spectroscopy to measure the battery’s resistance from its impedance.
Internal impedance measurement
Alternatively, one can estimate a battery’s SOH by measuring its internal impedance, which, just like internal resistance, rises as the battery ages. It can be done with the EIS method.
Although this technique shows a high level of accuracy, EIS can’t always meet the requirements of certain BMSs or match a battery’s operating conditions due to its complexity.
Methods working for both SOC and SOH
The following methods can be applied to estimate a battery’s state-of-charge and state-of-health simultaneously:
- Coulomb counting measures the rate at which a battery loses its capacity, which can be used to estimate its health loss. So, the technique works well for both metrics.
- Kalman filtering uses internal resistance, among other parameters to calculate the SOC. The same metric is required to estimate the battery’s SOH, so the algorithm can also simulate its aging.
- Neural networks can analyze a battery’s voltage, current, and temperature to predict its behavior including its SOC and SOH.
- Fuzzy logic models can measure the SOC and SOH based on abstract and approximate data as long as the model uses a high-performance microcontroller.
The best accuracy can be achieved by combining several methods – for example, neural networks with coulomb counting.
When participating in a complex BESS project, the team of Integra Sources used Kalman filter as a solution for measuring the SOC, and for a good reason.
Why Kalman filter as an optimal solution
Kalman filter is a recursive filter widely used to build engineering and macroeconomic models due to its ability to estimate dynamic systems states. By combining predicted states and noisy measurements, the filter represents a dynamic system as a mathematical model and predicts how the system will change the next moment.
The filter works in two steps. In the case of measuring a battery’s SOC, at the first stage, Kalman filter uses the input data to build a simulation of the processes occurring in the battery. The result is represented as a mathematical equation. At the second stage, the filter measures the actual parameters of the battery (namely voltage and current) and compares them with the values it has predicted. Then Kalman filter corrects the prediction. Thus, by using the current measurements and the previous state of the filter itself, Kalman filter can make quite precise estimations of a system’s state vector with a minimum margin of error.
Kalman filters are light on memory and very fast, which makes them perfect for real-time tasks, including battery management.
Kalman filter use case
Integra Sources was tasked with designing hardware and software for a battery management system that could estimate the battery’s state-of-charge. That included designing estimation algorithms, and after several tests, the team chose the central difference Kalman filter (CDKF).
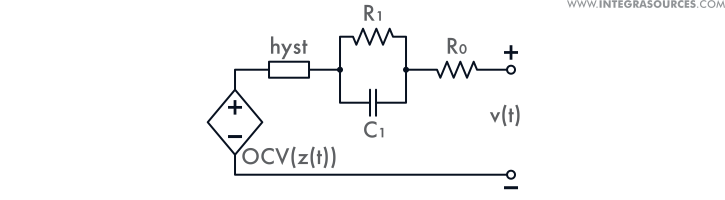
For the project, Integra used an equivalent-circuit model to simulate a battery cell’s internal processes. This is what its final version looks like:
Our next step was to compose the Kalman filter equation with the following variables:
- x = SOC (capacity + OCV + internal resistance + hysteresis + other values);
- f = part of the model that uses the input data (temperature and current) to calculate the present state from the previous one;
- y = theoretical output data (voltage) under the battery SOC (x) and input data (temperature and current);
- h = part of the battery’s model that uses the input data and the present state to calculate theoretical output data.
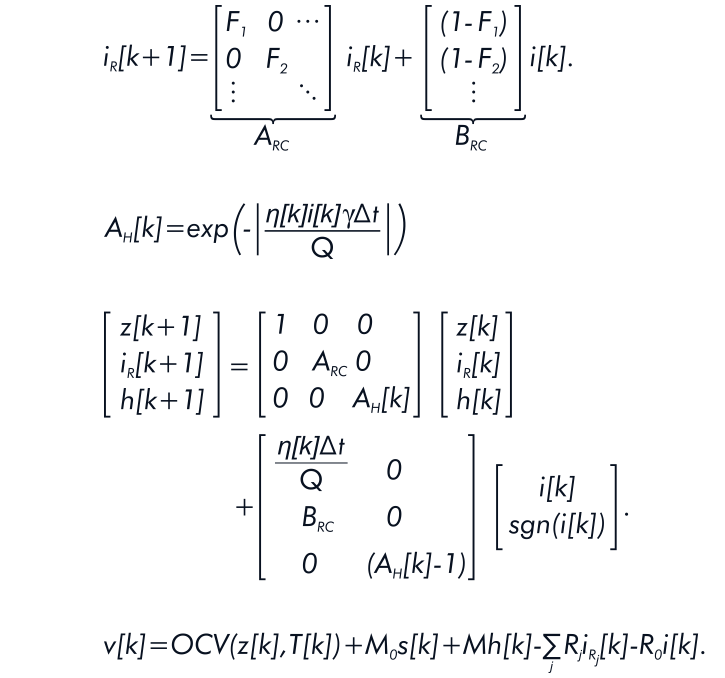
Then the team computed the Kalman gain matrix (L) and updated the state-estimate and error-covariance measurements.
This is what the final battery model equation looks like:
You can find the detailed solution of the equation on Integra Sources’ blog.
The methods used to measure the SOC and SOH demonstrate different levels of accuracy, as well as complexity and availability. An accurate but costly solution can hardly suit industrial production. That’s why developers and customers prefer combining several methods, which results in maximum accuracy at minimum expense.
Thanks to our expertise in battery management systems design, we at Integra Sources can help customers choose the most suitable methods of measuring battery state-of-charge, state-of-health, state-of-power, and state-of-energy. We also design BMS monitoring software and implement cell balancing to provide the best battery energy storage solutions.
About the author
Andrey Solovev, Chief Technology Officer, Integra Sources, Kazakhstan. He is the Co-founder and CTO at Integra Sources and earned his Ph.D. in Physics and Mathematics at Altai State University.